Question

he length of similar components produced by a company are approximated by a normaldistribution model with a mean of 5 cm and a standard deviation of 0.02 cm. If a component is chosen atrandoma)What is the probability that the length of this component is between 4.98 and 5.02?

Answer 1

Answer: 0.6826894

Explanation:

Given : The length of similar components produced by a company are approximated by a normal distribution model with a
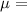`\mu=` 5 cm and a
`\sigma=`0.02 cm.

Let x be the random variable that represents the length of similar components produced by a company.

z-score :
`(x-\mu)/(\sigma)`

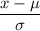
For x= 4.98

`(4.98-5)/(0.02)=-1`

For x= 5.02

`(5.02-5)/(0.02)=1`

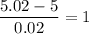
By using the standard z-value table (right -tailed) , the probability that the length of this component is between 4.98 and 5.02 will be :_

`P(4.98<x<62000)=P(-1<z<1)=1-2P(z>|1|)\ \ \\\\=1-2P(Z>|z|)]\\\\=1-2(0.1586553)\\\\=0.6826894`

Hence, the probability that the length of this component is between 4.98 and 5.02= 0.6826894