Answer:0.3 m/s
Step-by-step explanation:
Given
Length of ladder L=10 m
Foot of ladder is Pulled away at the rate of 0.4 m/s
Let the distance of foot of ladder be x m from origin and y be the distance of top of ladder from origin
from Pythagoras we can say that
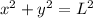
differentiating w.r.t time we get
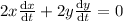
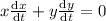
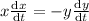
and at x=6m , y=8 m using Pythagoras
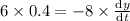
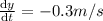
negative indicates that ladder is coming down