Question

Suppose we have a population whose proportion of items with the desired attribute is p = 0:5. (a) If a sample of size 200 is taken, find the probability that the proportion of successes in the sample will be between 0.47 and 0.51. Draw a sketch to help you solve this problem and use proper probability notation. (b) If a sample of size 100 is taken, find the probability that the proportion of successes in the sample will be between 0.47 and 0.51. Draw a sketch to help you solve this problem and use proper probability notation.

Answer 1

a. If a sample of size 200 is taken, the probability that the proportion of successes in the sample will be between 0.47 and 0.51 is 41.26%.

b. If a sample of size 100 is taken, the probability that the proportion of successes in the sample will be between 0.47 and 0.51 is 30.5%.

Explanation:

This problem should be solved with a binomial distribution sample, but as the size of the sample is large, it can be approximated to a normal distribution.

The parameters for the normal distribution will be

`\mu=p=0.5\\\\\sigma=√(p(1-p)/n) =√(0.5*0.5/200)= 0.0353`

We can calculate the z values for x1=0.47 and x2=0.51:

`z_1=(x_1-\mu)/(\sigma)=(0.47-0.5)/(0.0353)=-0.85\\\\z_2=(x_2-\mu)/(\sigma)=(0.51-0.5)/(0.0353)=0.28`

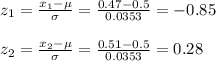
We can now calculate the probabilities:

`P(0.47<p<0.51)=P(-0.85<z<0.28)=P(z<0.28)-P(z<-0.85)\\\\P(z<0.28)-P(z<-0.85)=0.61026-0.19766=0.41260`

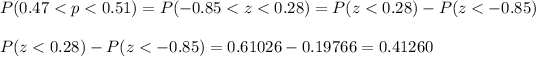
If a sample of size 200 is taken, the probability that the proportion of successes in the sample will be between 0.47 and 0.51 is 41.26%.

b) If the sample size change, the standard deviation of the normal distribution changes:

`\mu=p=0.5\\\\\sigma=√(p(1-p)/n) =√(0.5*0.5/100)= 0.05`

We can calculate the z values for x1=0.47 and x2=0.51:

`z_1=(x_1-\mu)/(\sigma)=(0.47-0.5)/(0.05)=-0.6\\\\z_2=(x_2-\mu)/(\sigma)=(0.51-0.5)/(0.05)=0.2`

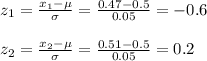
We can now calculate the probabilities:

`P(0.47<p<0.51)=P(-0.6<z<0.2)=P(z<0.2)-P(z<-0.6)\\\\P(z<0.2)-P(z<-0.6)=0.57926-0.27425=0.30501`

If a sample of size 100 is taken, the probability that the proportion of successes in the sample will be between 0.47 and 0.51 is 30.5%.