Question

In simplest radical form, what are the solutions to the quadratic eqaution 0=-3x^2-4x+5

Answer 1

`x= -(2+√(19) )/(3) \textrm { and } x = -(2-√(19) )/(3)`

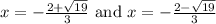
Explanation:

We have to find the solution of the quadratic single variable equation as given below:

- 3x² - 4x + 5 = 0 ..... (1)

The left-hand side can not be factorized.

So, apply The Sridhar Acharya Formula, which gives if ax² + bx + c = 0,the the solutions of the quadratic equation are

`x=\frac{-b + \sqrt{b^(2) -4ac} }{2a}` and,
`x=\frac{-b - \sqrt{b^(2) -4ac} }{2a}`

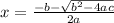
So, from the equation (1), we can write

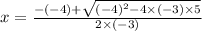`x= \frac{-(-4) +\sqrt{(-4)^(2)-4 * (-3) * 5 } }{2 * (-3)}` and

`x= \frac{-(-4) -\sqrt{(-4)^(2)-4 * (-3) * 5 } }{2 * (-3)}`

⇒
`x=(4+ 2√(19) )/(-6) \textrm{ and } x=(4-2√(19) )/(-6)`

⇒
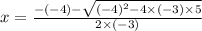
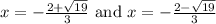`x= -(2+√(19) )/(3) \textrm { and } x = -(2-√(19) )/(3)` (Answer)