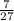Question

The probability of rain on any given day is 2/3 . What is the probability of at most one day of rain during the next three days?

Answer 1

`(7)/(27)`

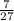
Explanation:

Let the event of raining on a day be success.

Then probability of success,
`p=(2)/(3)`

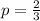
So, probability of failure is not raining on a day and is given as,

`q=1-p=1-(2)/(3)=(3-2)/(3)=(1)/(3)`

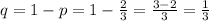
Now, number of days to check the probability of rain,
`n=3`

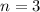
Now, probability of raining at most one day means number of success is either 0 or 1.

Using Bernoulli's distribution for
`X=0,1`

`P(X=0\textrm{ or }X=1)=_(0)^(3)\textrm{C}p^(0)q^(3-0)+_(1)^(3)\textrm{C}p^(1)q^(3-1)\\\\P(X=0\textrm{ or }X=1)=((1)/(3))^(3)+3((2)/(3))^(1)((1)/(3))^(2)\\\\P(X=0\textrm{ or }X=1)=(1)/(27)+(2)/(9)\\\\P(X=0\textrm{ or }X=1)=(1)/(27)+(6)/(27)\\\\P(X=0\textrm{ or }X=1)=(1+6)/(27)=(7)/(27)`

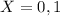
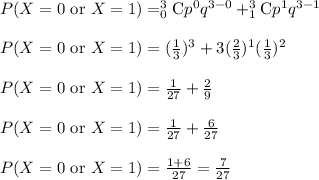
Therefore, the probability of at most one day of rain during the next three days is
`(7)/(27)`