Answer:
Part a)
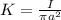
Part b)
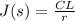
here we know that L = length of the wire
Step-by-step explanation:
Part a)
Current density is given as
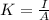
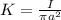
since current is uniformly divided across the crossection of the wire so it is given as
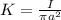
Part b)
As we know that volume current density is inversely proportional to the distance from the axis
So we will have
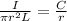
so we have
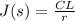
here we know that L = length of the wire