Answer:
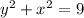
Explanation:
Let's take a general point P(x,y). If there is a right angle at P then the slopes of the lines passing through AP and BP must be perpendicular.
Two lines of slopes m1 and m2 are perpendicular if:
m1*m2=-1
The slope of the line passing through P(x,y) and A(3,0) is:
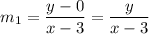
The slope of the line passing through P(x,y) and B(-3,0) is:
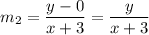
Substituting in the equation:
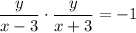
Operating:
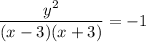

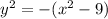
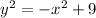
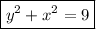
The locus is a circle centered at the origin with radius 3