The explicit formula is a(n) = 15(n – 10)
Solution:
Given, a term a(19) = 135 and common difference d = 15
We have to find the explicit formula.
Now, we know that, a(n) = a + (n – 1)d where a(n) is nth term, a is first term, d is common difference,
So, for a(19)
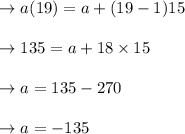
Now, we know that, an explicit formula is an expression for finding the nth term,
So, in our problem, expression for finding nth term is a + (n – 1)d
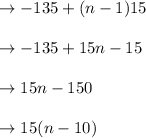
Hence, the explicit formula is a(n) = 15(n – 10).