Question

Helicopter blades withstand tremendous stresses. In addition to supporting the weight of a helicopter, they are spun at rapid rates and experience large centripetal accelerations, especially at the tip. (a) Calculate the magnitude (in m/s2) of the centripetal acceleration at the tip of a 3.10 m long helicopter blade that rotates at 280 rev/min. m/s2 (b) Compare the linear speed of the tip with the speed of sound (taken to be 340 m/s). vtip vsound =

Answer 1

Step-by-step explanation:

It is given that,

Length of the helicopter, l = 3.1 m

The helicopter rotates, the length of helicopter will become the radius of circular path, r = 3.1 m

Angular speed of the helicopter,
`\omega=280\ rev/min=29.32\ rad/s`

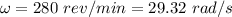
(a) The centripetal acceleration in terms of angular velocity is given by :

`a_c=r* \omega^2`

`a_c=3.1* (29.32)^2`

`a_c=2664.95\ m/s^2`

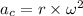
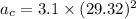
(b) Let v is the linear speed of the tip. The relation between the linear and angular speed is given by :

`v=r* \omega`

`v=3.1* 29.32`

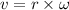
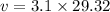
v = 90.89 m/s

`(v_(tip))/(v_(sound))=(90.89)/(340)=0.267`

Hence, this is the required solution.