Question

You are constructing a box from a piece of cardboard with dimensions 6 by 8 meters. You cut equal-size squares from each corner of the cardboard so you may fold the edges to construct the open top box. What are the dimensions of the box with the largest volume?

Answer 1

Length = 3.74 meters

Width = 5.74 meters

Height = 1.13 meters

Explanation:

Dimensions of the given piece of cardboard is 6 by 8 meters.

squares from each corner of the cardboard.

Then the dimensions of the box formed when folded

Length = (6 - 2x) meters

Width = (8 - 2x) meters

Height = x meters

Volume of the box = Length × width × height

Volume (V) = (6 - 2x)(8 - 2x)x

V = x(48 - 12x - 16x + 4x²)

V = 4x³ - 28x² + 48x

We take the derivative of Volume V

`(dV)/(dx)=(d)/(dx)(4x^(3)-28x^(2)+48x)`

`(dV)/(dx)=12x^(2)-56x+48`

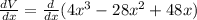
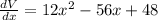
For maximum value,

`(dV)/(dx)=12x^(2)-56x+48=0`

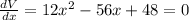
3x² - 14x + 12 = 0

`x=\frac{14\pm \sqrt{(14)^(2)-4(3)(12)}}{6}`

`x=(14\pm √(196-144))/(6)`

`x=(14\pm 7.2)/(6)`

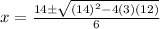
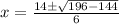
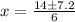
x = 3.53, 1.13

Now we have to check the value of x at which volume is maximum.

We take the second derivative of V

V" = 24x - 56

At x = 3.53

V" = 24(3.53) - 56 = 28.72

Since the value of V" is positive so the volume is not maximum at x = 3.53

At x = 1.13

V" = 24(1.13) - 56

V" = 27.2 - 56

= - 28.8 < 0

Therefore, for x = 1.13, volume will be maximum.

Now length of the box = 6 - 2(1.13) = 3.74 meters

width = 8 - 2(1.13) = 5.74 meters

And height of the box = 1.13 meters.