Question

Solve for x. Then find the side lengths of the triangle. If needed, round to the nearest tenth of a foot.

40 ft
Bx ft
6x ft
side lengths =
ft and

Answer 1

x=6

Sides= 36 & 18

Explanation:

Answer 2

The side lengths are 17.9 feet and 35.8 feet

Explanation:

Given lengths are;

40 feet, 3x feet and 6x feet

As the given triangle is right angled,

a = 3x, b = 6x and c = 40

Using Pythagorean theorem;

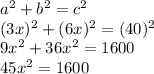`a^2+b^2=c^2\\(3x)^2+(6x)^2=(40)^2\\9x^2+36x^2=1600\\45x^2=1600\\`Dividing both sides by 45

`(45x^2)/(45)=(1600)/(45)\\x^2=35.55`

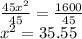
Taking square root on both sides

`√(x^2)=√(35.55)\\x=5.96`

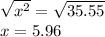
Side lengths = 3x = 3(5.96) = 17.9 feet

and

6x = 6(5.96) = 35.8 feet

Hence,

The side lengths are 17.9 feet and 35.8 feet