Question

If m<VST = (5x + 23) and m<VUT =
(8x - 49), find m<SVT​

Answer 1

Answer:17

Explanation:

Answer 2

37°

Explanation:

We know that
`\angle VST` and
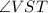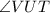`\angle VUT` are opposite angles in a quadrilateral.

If we assume that the quadrilateral is a parallelogram, then those angles are equal, so

`\angle VST = \angle VUT\\5x+23=8x-49`

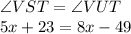
Then, we solve for
`x`

`23+49=8x-5x\\3x=72\\x=(72)/(3)\\ x=24`

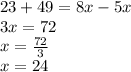
Now, we use this value to find VST angle

`\angle VST=5x+23=5(24)+23=143\°`

On the other hand, the sum of all four internal angles can be expressed as

`2(\angle VST)+2(\angle SVT)=360\°`

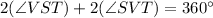
Solving for SVT

`2(143)+2(\angle SVT)=360\°\\\angle SVT = (360\° - 286\°)/(2)=37\°`

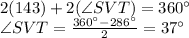
Therefore, the answer is 37°.