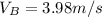Answer:
a)
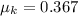 b)
b)
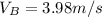
Step-by-step explanation:
In order to start solving this problem, we must begin by drawing a diagram of the situation (see attached picture).
On the diagram, we can identify three important points:
Point A=Starting point
Point B=Point where the block detaches from the spring.
Point C= Point where the block stops.
So in order to solve part a, we need to analyze the movement from point A to point C. We can do that by building an energy balance equation.
On point A there will only be potential energy while on point C there is no energy at all, since it was all wasted by the work done by the friction, so the equation will look like this:
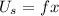
We know that the friction is defined to be the coefficient of kinetic friction times the normal force, so we can substitute that in our equation:
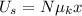
we can now solv this for the coefficient of kinetic friction so we get:
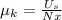
if we do a free body diagram of the block and do a sum of forces in the y-direction we get that:
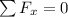
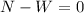
so
N=W
or
N=mg
we can substitute this into our coefficient of kinetic friction equation, so we get:
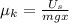
we know that the potential energy of a spring is given by:
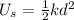
so we can substitute that also into our equation, so we get:
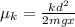
so now we can substitute data:
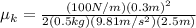
which yields:
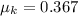
Once we have solved for the coefficient of kinetic friction, we can start solving part b:
b)
If we do an energy balance from point A to point B, we can see that in point A there will only be potential energy, while at point B there will be kinetic energy plut the energy lost due to the work done by the friction, so our equation looks like this:
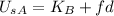
We can solve this equation for the kinetic energy, so we get:
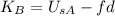
we know that the kinetic energy is defined to be one half of the mass times the square of the velocity. We also know what the potential energy of a spring is so we can substitute that into our equation, so we get:
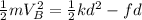
we can now multiply both sides of the equation by 2 so we get:
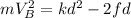
so now we can solve for the velocity, so we get:
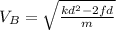
from the analysis done on the previous step, we know that the force of friction is given by the normal times the coefficient of kinetic friction, so we can use that in our equation to get:
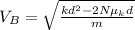
and we also know tha tthe normal is given by the weight of the block, so we can also substitute that:
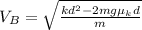
and now we can substitute all the values provided by the problem:
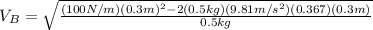
Which yields: