Answer:
(a) 17, 20, and 23.
(b) 299
(c)
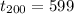 (Proved)
(Proved)
Explanation:
If we consider the sequence of numbers 2, 5, 8, 11, 14, ....... then it gives an A.P series with first trem(
 ) = 2 and the common difference(d) = 3.
) = 2 and the common difference(d) = 3.
(a) Therefore, the next three terms of the sequence will be 17, 20, and 23. (Answer)
(b) The 100th term of the sequence will be
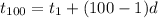
⇒
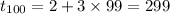 (Answer)
(Answer)
(c) So, the nth term of the A.P. will be given by
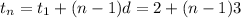 ..... (1)
..... (1)
Now, from equation (1) we get the 200th term as
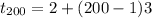
⇒
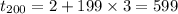 (Proved)
(Proved)