Question

A study looked at employee​ behavior, namely​ absenteeism, promptness to​ work, and turnover. The study found that 70​% of the employees had problems with​ absenteeism, also, 50​% had problems with turnover. Suppose that 40​% of the employees had problems with both absenteeism and turnover. Use this information to find the probability that an employee selected from the group surveyed had problems with either absenteeism or turnover.

Answer 1

There is a 40% probability that an employee selected from the group surveyed had problems with either absenteeism or turnover.

Explanation:

We can solve this problem building the Venn's diagram of these probabilities.

I am going to say that

The set A are those employees who had problems with absenteeism.

The set B are those employees who had problems with turnover.

We have that:

`A = a + (A \cap B)`

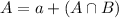
In which a represents those that had problems with absenteeism but not work turnover and
`(A \cap B)` are those who had problems with both these things.

By the same logic, we have that:

`B = b + (A \cap B)`

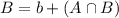
We start finding the values from the intersection of these sets:

Suppose that 40​% of the employees had problems with both absenteeism and turnover.

This means that
`A \cap B = 0.4`.

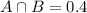50​% had problems with turnover

This means that
`B = 0.5`

`B = b + (A \cap B)`

`0.50 = b + 0.4`

`b = 0.10`

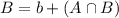
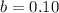
70​% of the employees had problems with​ absenteeism

This means that
`A = 0.7`

`A = a + (A \cap B)`

`0.70 = a + 0.4`

`a = 0.30`

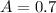
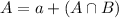
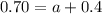
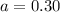
Use this information to find the probability that an employee selected from the group surveyed had problems with either absenteeism or turnover.

This is

`P = a + b = 0.30 + 0.10= 0.40`

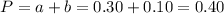
There is a 40% probability that an employee selected from the group surveyed had problems with either absenteeism or turnover.