Question

A model rocket is fired vertically upward from rest. Its acceleration for the first three seconds is a(t) = 60t at which time the fuel is exhausted and it becomes a freely "falling" body. Fourteen seconds later, the rocket's parachute opens, and the (downward) velocity slows linearly to -18 ft/s in 5 s. The rocket then "floats" to the ground at that rate.

At what time does the rocket reach its maximum height?
What is that height?
At what time does the rocket land?

Answer 1

(a) 8.4375 s

(b) 1409.06 ft

(c) 40.55 seconds

Step-by-step explanation:

v’(t)=a(t)=60t therefore

`v(t)=\int 60t=60\frac {t^(2)}{2}=30t^(2)`

`s(t)=\int v=\int 30t^(2)=30\frac {t^(3)}{3}=10t^(3)`

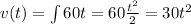
For first three seconds

`S(3)=10*3^(3)=270`

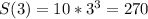
Since motion is vertical and we take upward direction as positive, acceleration is negative hence

a(t)=-32 and
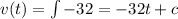`v(t)=\int -32=-32t+c` but since at t=0 then v=270 hence c=270

-32.2t+270=0 hence

t=270/32=8.4375 s

(b)

`s(t)=-16t^(2)+270t+B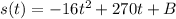` and since s(0)=270 then

`s(t)=-16t^(2)+270t+270`

`s(8.4375)=-16(8.4375)^(2)+270(8.4375)+270\approx 1409.06 ft`

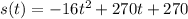
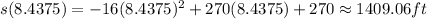
(c)

v(15)=-32(14)+270=-178 ft/s

`s(14)=-16(14)^(2)+270(14)+270=914 ft`

Average speed in the next 5 seconds becomes
`\frac {-178-18}{2}=-98 ft/s and s(5)=98(5)=490 ft`

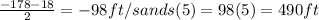
The altitude is 914-490=424 ft

`Time=\frac {424}{18}=23.6 seconds`

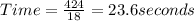
Time when rocket hits ground

Total time=3+14+23.6=40.55 seconds