Question

For a new product, you need to determine the average diameter of a specialized electronic component, which will be a critical component of the new product. You measure the diameter in a sample of size 15 and find an average diameter of 0.24 mm, with a standard deviation of 0.02 mm. Other studies indicate that the diameter of similar products is normally distributed. The 99% confidence interval for the average diameter of this electronic component is ______.

0.232 to 0.248
0.230 to 0.250
0.228 to 0.252
0.26 to 0.254
0.224 to 0.256

Answer 1

Answer: 0.224 to 0.256

Explanation:

As per given , we have

n= 15

df = 14 (df=n-1)

`\overline{x}=0.24\\ s=0.02`

Significance interval :
`\alpha: 1-0.99=0.01`

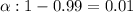
Since , population standard deviation is unknown , so we use t-test .

Using t-value table ,

`t_(df,\ \alpha/2)=t_(14,\ 0.005)=2.977`

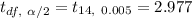
99% Confidence interval will be :

`\overline{x}\pm t_(df,\ \alpha/2)(s)/(√(n))`

`0.24\pm (2.977)(0.02)/(√(15))`

`\approx0.24\pm 0.015`

`=(0.24- 0.015,\ 0.24+ 0.015)=(0.225,\ 0.255)`

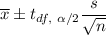
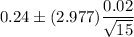
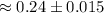
Hence, The 99% confidence interval for the average diameter of this electronic component is 0.225 to 0.255.

As we check all the given options , the only closest option is 0.224 to 0.256.

So the correct answer is 0.224 to 0.256.