Question

Which of the following has no solution?

(x + 1 < -1) ∩ (x + 1 < 1)
(x + 1 ≤ 1) ∩ (x + 1 ≥ 1)
(x + 1 < 1) ∩ (x + 1 > 1)

Answer 1

`(x+1<1)\cap (x+1>1)`

Explanation:

Solve all options.

1.
`(x+1<-1)\cap (x+1<1)`

`x+1<-1\Rightarrow x<-2\\ \\x+1<1\Rightarrow x<0`

So,

`(x+1<-1)\cap (x+1<1)\Rightarrow (x<-2)\cap (x<0)\Rightarrow (x<-2)`

There are solutions.

2.
`(x+1\le1)\cap (x+1\ge 1)`

`x+1\le 1\Rightarrow x\le 0\\ \\x+1\ge 1\Rightarrow x\ge 0`

So,

`(x+1\le 1)\cap (x+1\ge 1)\Rightarrow (x\le 0)\cap (x\ge 0)\Rightarrow (x=0)`

There is one solution.

3.
`(x+1<1)\cap (x+1>1)`

`x+1<1\Rightarrow x<0\\ \\x+1>1\Rightarrow x>0`

So,

`(x+1<1)\cap (x+1>1)\Rightarrow (x<0)\cap (x>0)\Rightarrow (x\in \emptyset)`

There are no solutions.

Answer 2

(x + 1 < 1) ∩ (x + 1 > 1)

Explanation:

When we have an interception relation, that means both sets have to have common solutions.

Let's solve the first inequality

`x + 1 < 1\\x<1-1\\x<0`

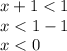
And the second one

`x + 1 > 1\\x>1-1\\x>0`

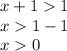
So, the interception would be

(x < 0) ∩ (x > 0)

This expression means the solution are the common areas of each region. However x < 0 expresses all numbers less than zero, and x > 0 expresses al number more than zero, as you can imagine, both sets of numbers don't have common solutions, because all numbers less than zero are different solutions of those which are more than zero.

So, we conclude the the third intersection is completely empty, because both sets don't intersect, that is, they don't have common solutions.