Given:
11.
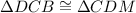
13.
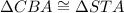
To find:
The missing values to complete the congruence statements:
11.
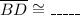
13.
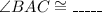
Solution:
11.
We have,
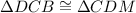
Here, vertices D, C, B are corresponding to C, D, M. So,
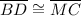
Therefore, the complete statement is
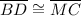 .
.
13.
We have,
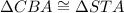
Here, vertices C, B, A are corresponding to S, T, A. So,

Therefore, the complete statement is
 .
.