If f(x)=3x-2 and g(x)=x^2+1, find f(g(-1)) and g(f(3))

Question

asked Jun 28, 2020 230k views

2 Answers

Berhane · Answer 1 · 2020-06-29T18:12:49+0000

If f(x)=3x-2 and g(x)=
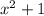x^2+1 , f(g(-1)) = 4, g(f(3)) = 50

Let's find those function values:

f(g(-1)):

First, find g(-1): g(-1) =
(-1)^2 + 1 = 2.

Now, plug g(-1) into f(x): f(g(-1)) = f(2) = 3(2) - 2 = 4.

g(f(3)):

First, find f(3): f(3) = 3(3) - 2 = 7.

Now, plug f(3) into g(x): g(f(3)) = g(7) =
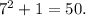
7^2 + 1 = 50.

Therefore:

f(g(-1)) = 4

g(f(3)) = 50

Ali Alqallaf · Answer 2 · 2020-07-04T03:36:48+0000

Answer:

f(g(-1))=4

g(f(3))=50

Explanation:

We know the definition of both functions:
f(x)=3x-2 , and
g(x)=x^2+1

A) In order to evaluate what
f(g(-1)) is , let's first investigate what g(-1) is using the definition for this function:

$g(x)=x^2+1\\g(-1)=(-1)^2+1\\g(-1)=1+1\\g(-1)=2$

Now let's find what f(2) is using f(x) definition:
$f(x)=3x-2\\f(2)=3(2)-2\\f(2)=6-2\\f(2)=4$

B) In order to evaluate what
g(f(3)) is , let's first investigate what f(3) is using the definition for this function:

$f(x)=3x-2\\f(3)=3(3)-2\\f(3)=9-2\\f(3)=7$

Now let's find what g(7) is using the definition for this function:

$g(x)=x^2+1\\g(7)=(7)^2+1\\g(7)=49+1\\g(7)=50$