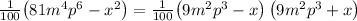Question

Write as a product:
1.44-a^12b^12
0.81p^6m^4-0.01x^2

Answer 1

`1.44 - a^(12) b^(12)=- (1)/(25) \left(5 a^(6) b^(6) - 6\right) \left(5 a^(6) b^(6) + 6\right)`

`(1)/(100) {\left(81 m^(4) p^(6) - x^(2)\right)} = (1)/(100) {\left(9 m^(2) p^(3) - x\right) \left(9 m^(2) p^(3) + x\right)}`

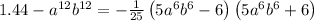
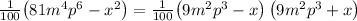
Explanation:

Factoring a polynomial involves writing it as a product of two or more polynomials. It reverses the process of polynomial multiplication.

Every polynomial that is a difference of squares can be factored by applying the following formula:

`a^2-b^2=(a+b)(a-b)`

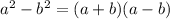
Note that a and b in the pattern can be any algebraic expression.

1. To express the polynomial
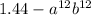`1.44 - a^(12)b^(12)` in factored form you must:

• Convert the decimal number 1.44 to a fraction

Rewrite the decimal number as a fraction with 1 in the denominator

`1.44 =  (1.44)/(1)`

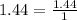
Multiply to remove 2 decimal places. Here, you multiply top and bottom by
`10^2 = 100`

`(1.44)/(1)*  (100)/(100)=  (144)/(100)`

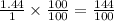
Find the Greatest Common Factor (GCF) of 144 and 100, and reduce the fraction by dividing both numerator and denominator by GCF = 4

`(144 / 4)/(100 / 4)=  (36)/(25)`

`1.44 - a^(12)b^(12)=(36)/(25) - a^(12) b^(12)`

• Factor the common term:

`{\left(- a^(12) b^(12) + (36)/(25)\right)} = {\left(- (1)/(25) \left(25 a^(12) b^(12) - 36\right)\right)`

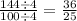
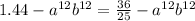
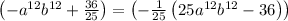
• Apply the difference of squares formula

`- (1)/(25) {\left(25 a^(12) b^(12) - 36\right)} = - (1)/(25) {\left(5 a^(6) b^(6) - 6\right) \left(5 a^(6) b^(6) + 6\right)}`

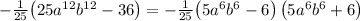
2. To express the polynomial
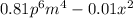`0.81p^6m^4-0.01x^2` in factored form you must:

• Convert the decimal numbers 0.81 and 0.01 to a fraction.

`0.81=(81)/(100)`

`0.01=(1)/(100)`

`0.81p^6m^4-0.01x^2=(81)/(100) m^(4) p^(6) - (x^(2))/(100)`

• Factor the common term:

`{\left((81)/(100) m^(4) p^(6) - (x^(2))/(100)\right)} = {\left((1)/(100) \left(81 m^(4) p^(6) - x^(2)\right)\right)}`

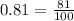
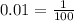
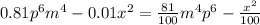
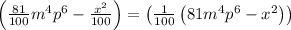
• Apply the difference of squares formula

`(1)/(100) {\left(81 m^(4) p^(6) - x^(2)\right)} = (1)/(100) {\left(9 m^(2) p^(3) - x\right) \left(9 m^(2) p^(3) + x\right)}`

Answer 2

see below

Explanation:

The factoring of the difference of squares is ...

r² -s² = (r -s)(r +s)

___

1) (1.2 -a^6b^6)(1.2+a^6b^6) . . . . . . . . r = 1.2, s = a^6b^6

2) (0.9p^3m^2 -0.1x)(0.9p^3m^2 +0.1x) . . . . . . . r = .9p^3m^2, s = 0.1x