Question

(1 point) Which of the following subsets of R3×3 are subspaces of R3×3? (R3×3 denotes the set of all 3×3 matrices with real entries.)A. The symmetric 3×3 matricesB. The 3×3 matrices whose entries are all integersC. The 3×3 matrices with all zeros in the third rowD. The 3×3 matrices in reduced row-echelon formE. The invertible 3×3 matricesF. The diagonal 3×3 matrices

Answer 1

For all the subset proposed, we have to ask ourself:

1. The sum of two such matrices is still that kind of matrix?
2. A scalar multiple of that kind of matrix is still a matrix of that kind?

So, we have:

A. The symmetric 3×3 matrices

Symmetric matrices are equal to their transpose. So, the multiple of a symmetric matrix is still symmetric, and the sum of two symmetric is still symmetric, because

`(\lambda A)^T = \lambda A^T,\quad (A+B)^T=A^T+B^T`

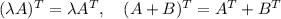
So, this is a subspace as well.

B. The 3×3 matrices whose entries are all integers

This is not a subspace, because we are allowed to use real scalars. So, if A is a matrix whose entries are all integers, we may pick an irrational scalar and we'd have, for example,
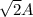`√(2)A`. The entries of this matrix are not integers, so the subset is not close under scalar multiplication, and thus it's not a subspace

C. The 3×3 matrices with all zeros in the third row

This is a subspace: if you multiply a matrix with a zero-row by a scalar, that row will remain zero. Similarly, if you sum two such matrices, the third row will result in a sum of zeroes.

D. The 3×3 matrices in reduced row-echelon form

This follows the same logic of case C: the zeroes remain where they are, so this is a subspace

E. The invertible 3×3 matrices

This is not a subspace: if A is invertible so is -A, but their sum A-A=0 is the null matrix, which is not invertible

F. The diagonal 3×3 matrices

This is a subspace: if A has nonzero elements only on the diagonal, so does
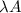`\lambda A`. Similarly, if A and B are diagonal, A+B will have non-zero addends only on the diagonal.