For all the subset proposed, we have to ask ourself:
- The sum of two such matrices is still that kind of matrix?
- A scalar multiple of that kind of matrix is still a matrix of that kind?
So, we have:
A. The symmetric 3×3 matrices
Symmetric matrices are equal to their transpose. So, the multiple of a symmetric matrix is still symmetric, and the sum of two symmetric is still symmetric, because

So, this is a subspace as well.
B. The 3×3 matrices whose entries are all integers
This is not a subspace, because we are allowed to use real scalars. So, if A is a matrix whose entries are all integers, we may pick an irrational scalar and we'd have, for example,
 . The entries of this matrix are not integers, so the subset is not close under scalar multiplication, and thus it's not a subspace
. The entries of this matrix are not integers, so the subset is not close under scalar multiplication, and thus it's not a subspace
C. The 3×3 matrices with all zeros in the third row
This is a subspace: if you multiply a matrix with a zero-row by a scalar, that row will remain zero. Similarly, if you sum two such matrices, the third row will result in a sum of zeroes.
D. The 3×3 matrices in reduced row-echelon form
This follows the same logic of case C: the zeroes remain where they are, so this is a subspace
E. The invertible 3×3 matrices
This is not a subspace: if A is invertible so is -A, but their sum A-A=0 is the null matrix, which is not invertible
F. The diagonal 3×3 matrices
This is a subspace: if A has nonzero elements only on the diagonal, so does
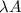 . Similarly, if A and B are diagonal, A+B will have non-zero addends only on the diagonal.
. Similarly, if A and B are diagonal, A+B will have non-zero addends only on the diagonal.