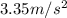Question

In a "worst-case" design scenario, a 2000-{\rm kg} elevator with broken cables is falling at 4.00{\rm m/s} when it first contacts a cushioning spring at thebottom of the shaft. The spring is supposed to stop the elevator,compressing 2.00 {\rm m} as it does so. During the motion a safety clampapplies a constant 17000-{\rm N} frictional force to the elevator.

1. What is the speed of the elevator after it has moveddownward 1.00 {\rm m} from the point where it first contacts aspring?
2. When the elevator is 1.00 {\rm m} below point where it first contacts a spring, whatis its acceleration?

Answer 1

v=3.73m/s,
`a=3.35m/s^(2)`

Step-by-step explanation:

In order to solve this problem, we must first draw a diagram that will represent the situation (See attached picture).

So there are two ways in which we can solve this proble. One by using integrls and the other by using energy analysis. I'll do it by analyzing the energy of the system.

So first, we ned to know what the constant of the spring is, so we can find it by analyzing the energy on points A and C. So we get the following:

`K_(A)+U_(Ag)=K_(C)+U_(Cs)+U_(Cg)+W_(Cf)`

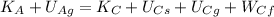
where K represents kinetic energy, U represents potential energy and W represents work.

We know that the kinetic energy in C will be zero because its speed is supposed to be zero. We also know the potential energy due to the gravity in C is also zero because we are at a height of 0m. So we can simplify the equation to get:

`K_(A)+U_(Ag)=U_(Cs)+W_(Cf)`

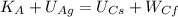
so now we can use the respective formulas for kinetic energy and potential energy, so we get:

`(1)/(2)mV_(A)^(2)+mgh_(A)=(1)/(2)ky_(C)+fy_(C)`

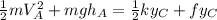
so we can now solve this for k, which is the constant of the spring.

`k=(mV_(A)^(2)+mgh_(A)-fy_C)/(y_(C)^(2))`

and now we can substitute the respective data:

`k=((2000kg)(4m/s)^(2)+(2000kg)(9.8m/s^(2))(2m)-(17000N)(2m))/((2m)^(2))`

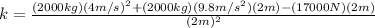
Which yields:

k= 9300N/m

Once we got the constant of the spring, we can now find the speed of the elevator at point B, which is one meter below the contact point, so we do the same analysis of energies, like this:

`K_(A)+U_(Ag)=K_(B)+U_(Bs)+U_(Bg)+W_(Bf)`

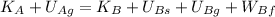
In this case ther are no zero values to eliminate so we work with all the types of energies involved in the equation, so we get:

`(1)/(2)mV_(A)^(2)+mgh_(A)=(1)/(2)mV_(B)^(2)+(1)/(2)ky_(B)^(2)+mgh_(B)+fy_(B)`

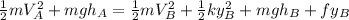
and we can solve for the Velocity in B, so we get:

`V_(B)=\sqrt{(mV_(A)^(2)-ky_(B)^(2)+2mgh_(B)-2fy_(B))/(m)}`

we can now input all the data directly, so we get:

`V_(B)=\sqrt{((2000kg)(4m/s)^(2)-(9300N/m)(1m)^(2)+2(2000kg)(9.8m/s^(2))(1m)-2(17000N)(1m))/((2000kg))}`

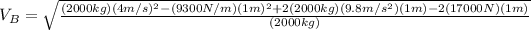
which yields:

`V_(B)=3.73m/s`

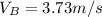
which is the first answer.

Now, for the second answer we need to find the acceleration of the elevator when it reaches point B, for which we need to build a free body diagram (also included in the attached picture) and to a summation of forces:

`\sum F=ma`

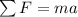
so we get:

`F_(s)+f-W=ma`

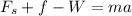
Supposing the acceleration is positive when it points upwards.

So we can solve that for the acceleration, so we get:

`a=(F_(s)+f-W)/(m)`

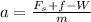
or

`a=(ky_(B)+f-W)/(m)`

and now we substitute the data we know:

`a=((9300N/m)(1m)+(17000N)-(2000kg)(9.8m/s^(2)))/(2000kg)`

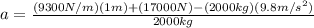
which yields:

`3.35m/s^(2)`