Answer:
The number of water that must be mixed in the solution is 170.27 mL
Step-by-step explanation:
given information :
Temperature of water (
 ) =
) =
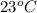
density of water (ρ) = 1.00 g/mL
Temperature of coffee (
 ) =
) =
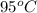
volume of coffee (
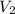 ) = 180 mL
) = 180 mL
Mixed Temperature (
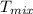 ) =
) =
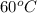
to calculate the heat, w use the formula :
Q = m x c x ΔT
where
m = mass of the substance (g)
c = specific heat (J/
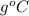 )
)
ΔT = the temperature change (
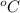 )
)
in the mixture solution, the heat of the water (
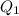 ) should be the same as the heat of coffee (
) should be the same as the heat of coffee (
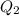 ). Thus,
). Thus,
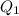 =
=
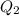
 x
x
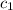 x Δ
x Δ
 =
=
 x
x
 x Δ
x Δ

where
 is the mass of water
is the mass of water
 is the mass of coffee
is the mass of coffee
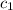 is the specific heat of water
is the specific heat of water
 is the specific heat of coffee
is the specific heat of coffee
Assume coffee and water have the same specific heat. So,
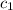 =
=
 , we can remove it from the equation.
, we can remove it from the equation.
Hence.
 x Δ
x Δ
 =
=
 x Δ
x Δ

we know that
ρ =
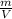
m = ρ x V, subtitute it to the equation:
ρ
 x V
x V
 x Δ
x Δ
 = ρ
= ρ
 x V
x V
 x Δ
x Δ

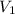 is the volume of water
is the volume of water
coffee and water have the same density, so we can remove the formula
V
 x Δ
x Δ
 = V
= V
 x Δ
x Δ

V
 = (V
= (V
 x Δ
x Δ
 ) / Δ
) / Δ

V
 = V
= V
 x (
x (
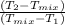
V
 = 180 mL x
= 180 mL x
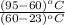
V
 = 180 mL x
= 180 mL x
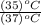
V
 = 170.27 mL
= 170.27 mL