Answer:
1) 0.487,0.0436
2) 56.3 cm
Explanation:
Let X be the scores ranging from 0 to 20 of the Psychology students at Wittenberg University completed the Dental Anxiety Scale questionnaire.
X is N(11,3.5)
a) the probability that someone scores between a 10 and a 15 on the Dental Anxiety Scale.
=
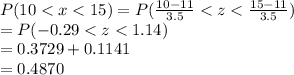
b)
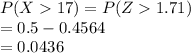
c) Y is N(50, 20) where Y is tree diameter at breast height 110 years after the fire.
P(X>d) = 0.30
Corresponding Z value = 0.525
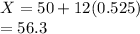
d = 56.3 cm