Question

A research engineer for a tire manufacturer is investigating tire life for a new rubber compound. She has built 10 tires and tested them to end-of-life in a road test. The sample mean and standard deviation are 61,492 and 2990 kilometers, respectively. Assume population is approximately normally distributed. (a) Can you conclude, using =0.05, that the standard deviation of tire life exceeds 3000 km ? yes ot no ?

Answer 1

The standard deviation of tire life does exceed 3000 km

Explanation:

This is a Chi-Square Hypothesis Test for the Standard Deviation, here we have

`\bf H_0: \sigma = 3000`

`\bf H_a: \sigma > 3000`

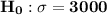
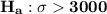
so, this is an upper one-tailed test.

The test statistic is

`\bf T=((n-1)s^2)/(\sigma^2)`

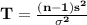
where

n = 10 is the sample size

s = sample standard deviation

`\bf \sigma` = population standard deviation

we would reject the null hypothesis if

`\bf T>\chi^2_((\alpha,n-1))`

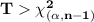
where

`\bf \chi^2_((\alpha,n-1))`

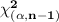
is the critical value corresponding to the level of significance
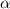`\bf \alpha` with n-1 degrees of freedom.

we can use either a table or a spreadsheet to compute this value.

In Excel use

CHISQ.INV(0.05,9)

In OpenOffice Calc use

CHISQINV(0.05;9)

and we get this value equals 3.3251

Working out our T statistic

`\bf T=((n-1)s^2)/(\sigma^2)=(9*(2990)^2)/((3000)^2)=8.9401`

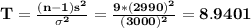
Since T > 3.3251 we reject the null and conclude that the standard deviation of tire life exceeds 3000 km.