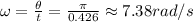Question

When a slice of buttered toast is accidentally pushed over the edge of a counter, it rotates as it falls. Suppose the distance to the floor is 89 cm and the toast rotates less than 1 rev. (a) What is the smallest angular speed that causes the toast to hit and then topple to be butter-side down?

Answer 1

7.38 rad/s

Step-by-step explanation:

Assume no air resistance, we can first calculate the time it takes for the toast to be dropped 0.89m to the floor. Since we have

`h = (gt^2)/(2)`

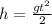
where
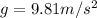`g = 9.81m/s^2` and h = 0.89 m

`t^2 = (2h)/(g) = (2*0.89)/(9.81) \approx 0.181`

`t = √(0.811) \approx 0.426 s`

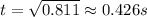
This is also the time for the toast to flip one time at a constant angular speed. The angle it covered would be at
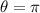`\theta = \pi` radian.

So the smallest angular speed it needs to hit and topple butter-side down is

`\omega = (\theta)/(t) = (\pi)/(0.426) \approx 7.38 rad/s`