Question

The Intelligence Quotient (IQ) test scores are normally distributed with a mean of 100 and a standard deviation of 15. You enrolled in a class of 25 students. What is the probability that the class' average IQ exceeds 130?

Answer 1

The required probability is 0.0228

Explanation:

Consider the provided information.

Mean of 100 and a standard deviation of 15. You enrolled in a class of 25 students.

Therefore,
`\mu =100,\sigma 15`

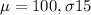
We want the probability that the class' average IQ exceeds 130

As we know:
`z=(\bar x -\mu)/(\sigma)`

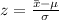
Substitute the respective value as shown:

`z=(130 -100)/(15)`

`z=(30)/(15)`

`z=2`

`P(z>2)=1-P(z<2)`

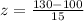
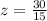
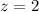
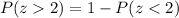
Now by using z table:

`P(x>130)=P(z>2)=1-0.9772`

`P(x>130)=0.0228`

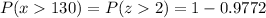
Hence, the required probability is 0.0228