Question

A quality engineer in a light bulb factory is planning a study to estimate the average life of a large shipment of light bulbs. The engineer wants to estimate the average life within plus or minus 15 hours with 95 percent confidence. Assuming a process standard deviation of 100 hours, determine the sample size for this study

Answer 1

The required sample size is 171.

Explanation:

Consider the provided information.

The engineer wants to estimate the average life within plus or minus 15 hours with 95 percent confidence. Assuming a process standard deviation of 100 hours,

First calculate the value of
`Z_{(\alpha)/(2)}`

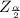
By using the table we get.

`Z_{(\alpha)/(2)}=1.96`

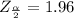
Now use the formula:
`N=(\frac{Z_{(\alpha)/(2)}* \sigma}{E})^2`

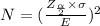
Substitute the respective values in the above formula we get.

`N=((1.96* 100)/(15))^2`

`N=((1.96* 100)/(15))^2`

`N=((196)/(15))^2=170.73777`

`N\approx171`

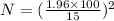
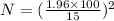
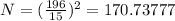
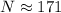
Hence, the required sample size is 171.