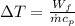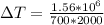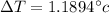Question

In the well-insulated trans-Alaska pipeline, the high viscosity of the oil and long distances cause significant pressure drops, and it is reasonable to question whether flow work would be significant. Consider an 150 km length of pipe of diameter 1.2 m, with oil flow rate 500 kg/s. The oil properties are 900 kg/m3, 2000 J/kg·K, 0.765 N·s/m2. Calculate the pressure drop, the flow work, and the temperature rise caused by the flow work. Recall from chapter 1, for steady flow, one inlet, one outlet, no heat transfer, no work, and negligible kinetic and protential energy changes, the enthalpy of the fluid remains constant. Enthalpy is the sum of internal energy and flow work.

Answer 1

Our values are defined by,

`L=150*10^3m`

`\Phi = 1.2m`

`\dot{m}=700kg/s`

`\rho_o=900km/m^3`

`Sp=2000J/KgK`

`\mu_k = 0.765Ns/m^2`

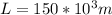
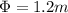
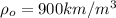
With this data we can easily calculate first the mean velocity of the flow,

The velocity is given by,

`\\u=\frac{\dot{m}}{\rho_o A_c}`

`\\u = \frac{\dot{m}}{\rho_o \pi/4\Phi^2}`

`\\u = (4*700)/(900\pi(1.2)^4)`

`\\u=0.688m/s`

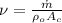
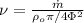
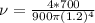
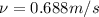
With the mean velocity is now possible determine if the flow is Laminar or turbulent, for that we need Number Reynolds.

Remember that a Laminar Flow is given when Reynolds number is minor to 2300, then

`Re_x = \frac{4\dot{m}}{\pi D\mu_k}`

`Re_x = (4*700)/(\pi*1.2*0.765)`

`Re_x = 970.8798`

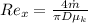
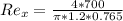
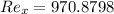
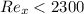`Re_x < 2300`, then the flow is laminar.

For this section we will consider the Pressure drop to calculate the flow Work and the Total Energy conservation of this flow.

To calculate the Pressure drop we need the Friction factor, which is given by,

`f= (64)/(Re)=(64)/(970.8789)`

`f= 0.06591`

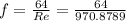
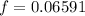
Then the Pressure drop is given by,

`\Delta P = (f\rho_o \\u^2 L)/(2D)`

`\Delta P = (0.06591*900*(0.688)^2*183*10^3)/(2*1.2)`

`\Delta P = 2.141*10^6Pa`

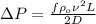
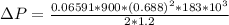
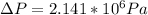
We can now calculate the Flow Work given by,

`W_f = \frac{\Delta P\dot{m}}{\rho_o}`

`W_f = (2.141*10^6*700)/(900)`

`W_f = 1.6651*10^6J`

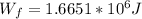
From energy conservation we have

`W_f=q`

`W_f = \dot{m}c_p\Delta T`

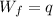
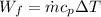
Re-arrange for
`\Delta T`

`\Delta T = \frac{W_f}{\dot{m}c_p}`

`\Delta T = (1.56*10^6)/(700*2000)`

`\Delta T = 1.1894\°c`