Question

A home improvement contractor is painting the walls and ceiling of a rectangular room. The volume of the room is 1584 cubic feet. The cost of wall paint is $0.06 per square foot and the cost of ceiling paint is $0.11 per square foot. Find the room dimensions that will minimize the cost of the paint. (Enter your answers as a comma-separated list.) Incorrect: Your answer is incorrect. ft

Answer 1

The room dimensions that will minimize the cost of the paint are 12 ft x 12 ft x 11 ft.

Explanation:

We can find first the volume equation using the formula of the volume of a box.

`V= xyz`

Thus we get the constraint function

`1584 = xyz`

Then since we are asked to minimize the cost, we can write the cost function which is the area of each one of the walls and ceiling multiplied by the painting cost.

`C=0.11 xy+ 2(0.06)xz+2(0.06yz \\ C =0.11 xy+0.12xz+0.12yz`

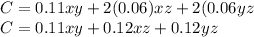
Lagrange Multipliers to find minimum cost.

We can continue finding the partial derivatives to build the system of equations required for Lagrange Multipliers method.

`C_x=\lambda V_x \\ C_y = \lambda V_y \\ C_z = \lambda V_z`

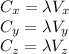
And the constraint function

`xyz=1584`

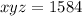
So we get

`0.11y+0.12z=\lambda yz \\ 0.11x+0.12z=\lambda xz \\ 0.12x+0.12y=\lambda xy\\ xyz=1584`

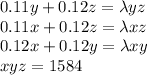
We can multiply each side of each equation by the dimension which is missing to get the full volume on the right side.

`0.11xy+0.12xz=\lambda xyz \\ 0.11xy+0.12yz=\lambda xyz \\ 0.12xz+0.12yz=\lambda xyz`

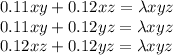
Then we can set each the equations equal to each other, so from the first one and the second equation we get

`0.11xy+0.12xz= 0.11xy+0.12yz`

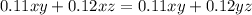
We can subtract 0.11xy from both sides.

`0.12xz=0.12yz`

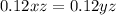
And we can divide both sides by 0.12z to get

`x=y`

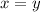
We can repeat the process by setting the first and third equation equal to each other.

`0.11xy+0.12xz= 0.12xz+0.12yz`

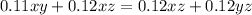
We can subtract 0.12 xz from both sides

`0.11xy=0.12yz`

And we can solve by z

`z= \cfrac{0.11x}{0.12}\\ z = \cfrac{11x}{12}`

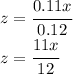
So if we replace that as well y = x on the constraint for the volume euqation we get

`1584=x(x)\left(\cfrac{11}{12}x\right) \\ 1584=\cfrac{11}{12}x^3`

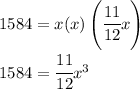
We can then solve for x

`x^3 = \cfrac{1584(12)}{11}`

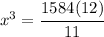
And taking the cube root

`x = \sqrt[3]{\cfrac{1584(12)}{11}}`

`x = \sqrt[3]{1728}`

`x=12 ft`

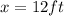
So then we can use the equations we have found for y and z in terms of x

`y = x \\ y = 12 ft`

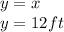
And

`z= \cfrac{11x}{12}\\z= \cfrac{11(12)}{12} \\ z=11ft`

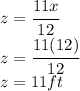
Then the dimensions of the room that will minimize the cost are 12ft x 12 ft x 11 ft. Since you have to enter using commas you can write 12, 12, 11, please check as well if you have to insert the units that are feet for each.