Question

A rectangular storage container with open top is to have a volume of 50 ft3 . The length of the base of the container is to be twice its width. Material for the sides costs $5 per square foot, and materials for the base cost $8 per square foot. Find the dimensions that minimize the cost of the material for the box.

Answer 1

Length = 2.862 ft

Width = 1.431 ft

Height = 3.05 ft

Step-by-step explanation:

Let L be lenght, W be width, and H be height of the storage container. Since length is to be twice the width, it means L = 2W. The volumn of the container would also be:

`V = LWH = L(2L)H = 2L^2H`

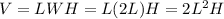
SInce the volumn constraint is 50, that means:

`2L^2H = 50`

`H = (25)/(L^2)`

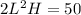
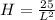
The cost for the base would be its area times unit price

`C_b = A_bU_b = LWU_b = 2L^2U_b = 2*8L^2 = 16L^2`

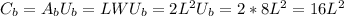
Likewise, the cost for the sides would be

`C_s = A_sU_s = 2(L+W)HU_s = 6LH5 = 30LH`

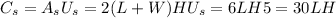
We can substitute H from the equation above:

`C_s = 30L(25)/(L^2) = (750)/(L)`

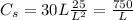
Therefore the total material cost

`C = C_b + C_s = 16L^2 + (750)/(L)`

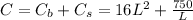
To find the minimum of this function, we can take first derivative then set to 0:

`C^(') = (16L^2)^(') + ((750)/(L))^(') = 0`

`32L - (750)/(L^2) = 0`

`32L = (750)/(L^2)`

`L^3 = 750/32 = 23.4375`

`L = 23.4375^(1/3) \approx 2.862ft`

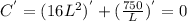
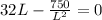
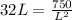
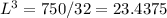
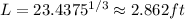
So W = L/2 = 1.43ft and

`H = (25)/(L^2) = 3.05 ft`

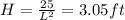
If we take the 2nd derivative and substitute L = 2.862 we would have

`C{''} = 32 + 2(750)/(L^3) = 32 + (1500)/(23.43) = 96 > 0`

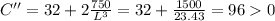
Hence L = 2.862 would yield the minimum material cost