Answer:
Length = 2.862 ft
Width = 1.431 ft
Height = 3.05 ft
Step-by-step explanation:
Let L be lenght, W be width, and H be height of the storage container. Since length is to be twice the width, it means L = 2W. The volumn of the container would also be:

SInce the volumn constraint is 50, that means:
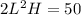
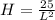
The cost for the base would be its area times unit price
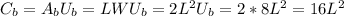
Likewise, the cost for the sides would be
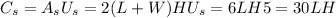
We can substitute H from the equation above:
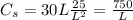
Therefore the total material cost
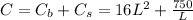
To find the minimum of this function, we can take first derivative then set to 0:
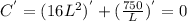

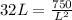
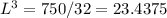
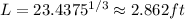
So W = L/2 = 1.43ft and
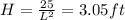
If we take the 2nd derivative and substitute L = 2.862 we would have
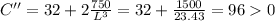
Hence L = 2.862 would yield the minimum material cost