Answer:
The other factors are (4x + 7) and (4x - 7).
Explanation:
One of the factor of the polynomial
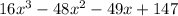 is given to be (x - 3). We have to find the other factors of this polynomial.
is given to be (x - 3). We have to find the other factors of this polynomial.
Now,
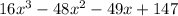
=
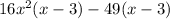
=

=
![(x - 3)[(4x)^(2) - 7^(2)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/sg5eo6ylkzh3ora9egh9648rqwhr91ymx1.png) {Since we know the formula,
{Since we know the formula,
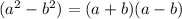 }
}
=

Therefore, the other factors are (4x + 7) and (4x - 7). (Answer)