A Michelson interferometer uses red light with a wavelength of 656.45 nm from a hydrogen discharge lamp. Part A How many bright-dark-bright fringe shifts are observed if mirror …

Question

asked Oct 17, 2020 209k views

1 Answer

Bilal Ahmad · Answer 1 · 2020-10-22T21:37:52+0000

Answer:

51793 bright-dark-bright fringe shifts are observed when the mirror M2 moves through 1.7cm

Step-by-step explanation:

The number of maxima appearing when the mirror M moves through distance \Delta L is given as follows,

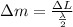
$\Delta m = (\Delta L)/((\lambda)/(2))$

Here,

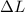$\Delta L$ = is the distance moved by the mirror M

$\lambda$ is the wavelenght of the light used.

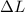$\Delta L$ = 0.017m

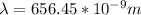
$\lambda = 656.45*10^(-9)m$

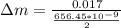
$\Delta m = (0.017)/((656.45*10^(-9))/(2))$

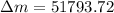
$\Delta m = 51793.72$

Therefore, 51793 bright-dark-bright fringe shifts are observed when the mirror M2 moves through 1.7