Question

A coil with 25 turns of wire is moving in a uniform magnetic field of 1.5 T. The magnetic field is perpendicular to the plane of the coil. The coil has a crosssectional area of 0.80 m2

. The coil exits the field in 1.0 s.
Find the induced emf.

Answer 1

Given that,

Number of turns, N = 25

Magnetic field, B = 1.5 T

The coil has a crosssectional area of 0.80 m2

The coil exits the field in 1.0 s.

To find,

Induced emf in the coil.

Solution,

The induced emf in the coil is given by :

`\epsilon=(-d\phi)/(dt)\\\\=(dB)/(dt)\\\\=(NBA)/(t)\\\\=(25* 1.5* 0.8)/(1)\\\\=30\ V`

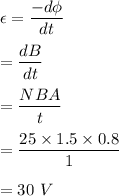
So, the induced emf in the coil is 30 V.