Question

A newly discovered planet has twice the mass of the Earth, but the acceleration due to gravity on the new planet’s surface is exactly the same as the acceleration due to gravity on the Earth’s surface. What is the radius Rp of the new planet in terms of the radius R of Earth?

Answer 1

The radius of the newly discovered planet with twice the mass of Earth and the same acceleration due to gravity is √2 times the radius of Earth.

Step-by-step explanation:

To answer the question regarding the radius Rp of a newly discovered planet with twice the mass of Earth and the same acceleration due to gravity, we need to use the gravitation equation:

Fgravity =
`G * (m1*m2) r^(2)`,

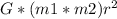where Fgravity is the gravitational force, G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between the centers of the two masses.

In this case, the acceleration due to gravity on both planets is the same. Hence, we can equate the gravitational force experienced on Earth to that experienced on the newly discovered planet which has twice the mass of Earth. We get:

`G * (mass of Earth * mass of object) / (radius of Earth)^(2)` =
`G * (2 * mass of Earth * mass of object) / (radius of new planet)^(2)`

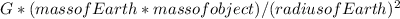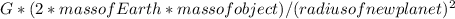
By cancelling out the common terms and simplifying, we find that:

(radius of new planet) = √2 * (radius of Earth).

Therefore, the radius of the new planet is √2 times the radius of Earth.