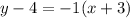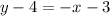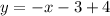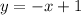Answer with Step-by-step explanation:
We are given that
P(-7,0) and Q(1,8)
We have to find the midpoint of PQ and write an equation of the line that passes through the midpoint.
Mid-point formula:
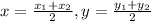
By using this formula ,
The mid point of PQ
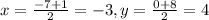
Hence, the midpoint of PQ is (-3,4).
Slope of PQ=
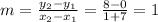
Slope of perpendicular line=
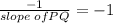
The equation of line which is passing through the point (-3,4) with slope -1 is given by

The equation of line which is passing through the point (-3,4) with slope -1 is given by