Answer:
a) The 95% CI for the mean is
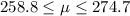 .
.
The value 274 is plausible because it is within the limits of the CI.
b) We can not reject the hypothesis
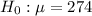
c) They are consistent. The conclusion from both results is that 274 could be the real mean. In both cases we couldn't prove 274 it is not the mean.
Explanation:
In this problem we have a sample of n=32 with mean M=266.8 and standard deviation s=22.
a) To compute a 95% confidence interval (CI), we calculate
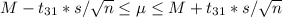
First we have to estimate t, with 32-1=31 degrees of freedom for a two-tailed 95% CI.
By looking up in the t-table, we get t=2.0395.
Then the confidence interval is
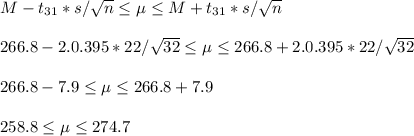
b) We have to test the hypothesis
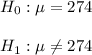
The significance level is 0.05.
We calculate the t-statistics:

The p-value for t=1.84 and df=31 is P=0.07536.
As P=0.07 is greater than the significance level (0.05), we can not reject the null hypothesis. The interpretation of this is we can not claim that the mean is not 274.