Question

A proton starting from rest travels through a potential of 1.0 kV and then moves into a uniform 0.040-T magnetic field. What is the radius of the proton's resulting orbit? (mproton = 1.67 × 10-27 kg, e = 1.60 × 10-19 C) A proton starting from rest travels through a potential of 1.0 kV and then moves into a uniform 0.040-T magnetic field. What is the radius of the proton's resulting orbit? (proton = 1.67 × 10-27 kg, = 1.60 × 10-19 C) 0.14 m 0.11 m 0.080 m 0.19 m 0.17 m

Answer 1

r = 0.11 m

Step-by-step explanation:

Let's suppose that the magnetic field is perpendicular to the vector speed. In that case, the centripetal force would be the same as the Lorentz force.

`F=ma_(c)=qvB`

`m(v^(2))/(r)=qvB`.

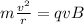Solving this equation for r, we will have:

`r=(mv)/(qB)`

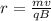
Now, to find r we need to get the speed of the particle. Let's use the law of conservation of energy. The kinetic energy is equal to the electric potential energy:

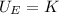`U_(E)=K`, but
`U_(E)=qV`

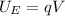
So we would have:

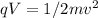`qV=1/2mv^(2)`, then
`v=\sqrt{(2qv)/(m)}`

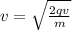
Finally
`r = m\frac{\sqrt{(2qv)/(m)}}{qB}= 0.11 m`

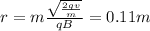
Have a nice day!