Answer:
The first affirmation is true.
The second one is false.
Explanation:
The confidence interval of a sample of a measure with mean M and a standard deviation of
 is given by:
is given by:
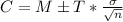 .
.
In which
 is the length of the sample.
is the length of the sample.
Here, the value that is related to the width of the interval is T. The lesser T is, the narrower the interval is.
However, when we look at the t-table to find the value of T, we see that as the confidence level increases, so does the value of T. This means that as the confidence level increases, so does the width of the interval.
The confidence interval was too wide to provide a precise estimate. The students are strategizing about how to produce a narrower confidence interval.
This is true, when a confidence interval is too wide to provide a precise estimate, it needs to be narrowed.
The students could produce a narrower confidence interval by increasing the confidence level to 95%.
As explained above, the interval gets wider as the confidence level is increse.
This means that the affirmation is false.