Question

An electron of mass 9.11 1031 kg has an initial speed of 3.00 105 m/s. It travels in a straight line, and its speed increases to 7.00 105 m/s in a distance of 5.00 cm. Assuming its acceleration is constant, (a) determine the force exerted on the electron and (b) compare this force with the weight of the electron, which we ignored.

Answer 1

Step-by-step explanation:

It is given that,

Mass of an electron,
`m=9.11* 10^(-31)\ kg`

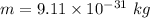
Initial speed of the electron,
`u=3* 10^5\ m/s`

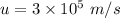
Final speed of the electron,
`v=7* 10^5\ m/s`

Distance, d = 5 cm = 0.05 m

(a) The acceleration of the electron is calculated using the third equation of motion as :

`a=(v^2-u^2)/(2d)`

`a=((7* 10^5)^2-(3* 10^5)^2)/(2* 0.05)`

`a=4* 10^(12)\ m/s^2`

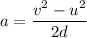
Force exerted on the electron is given by :

`F=m* a`

`F=9.11* 10^(-31)* 4* 10^(12)`

`F=3.64* 10^(-18)\ N`

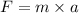
(b) Let W is the weight of the electron. It can be calculated as :

`W=mg`

`W=9.11* 10^(-31)* 9.8`

`W=8.92* 10^(-30)\ N`

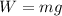
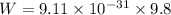
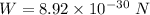
Comparison,

`(F)/(W)=(3.64* 10^(-18))/(8.92* 10^(-30))`

`(F)/(W)=4.08* 10^(11)`

Hence, this is the required solution.