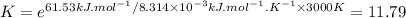Question

The decomposition of a generic diatomic element in its standard state is represented by the equation 12X2(g)⟶X(g) Assume that the standard molar Gibbs energy of formation of X(g) is 4.84 kJ·mol−1 at 2000 . K and −61.53 kJ·mol−1 at 3000 . K. Determine the value of the thermodynamic equilibrium constant, K , at each temperature. At 2000 . K, Δ????f=4.84 kJ·mol−1 . What is K at that temperature?

Answer 1

At 2000 K. K: 0.747

At 3000 K. K: 11.79

Step-by-step explanation:

Let's consider the decomposition of a generic diatomic element in its standard state.

1/2 X₂(g) ⟶ X(g)

The relation between the equilibrium constant (K) and the standard Gibbs energy (ΔG°) is:

`K = e^(-\Delta G  \° / R.T)`

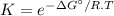
where,

R is the ideal gas constant (8.314 × 10⁻³ kJ/mol.K)

T is the absolute temperature

At 2000 K (ΔG° = 4.84 kJ·mol⁻¹)

`K=e^{-4.84kJ.mol^(-1)/8.314 * 10^(-3) kJ.mol^(-1).K^(-1) * 2000 K } =0.747`

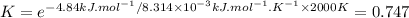
At 3000 K (ΔG° = −61.53 kJ·mol⁻¹)

`K=e^{61.53kJ.mol^(-1)/8.314 * 10^(-3) kJ.mol^(-1).K^(-1) * 3000 K } =11.79`