Question

A website tracks advanced exam registrations and performance by high school students. In a recent year, of the students who took the microeconomics exam, 44 % passed. In an attempt to determine if the proportion of those passing the advanced math and science exams is equal to the 44% success rate for microeconomics, a random sample of 250 students enrolled in advanced math and science classes has been selected. Complete parts a and b below. a. If 26 of the students in the sample passed at least one advanced math or science exam, calculate the proportion of those students who passed at least one math or science exam. Does this statistic indicate that the proportion of students who passed at least one advanced math or science exam is less than the 44% success rate for microeconomics? Support your assertion. The proportion of those students who passed at least one math or science exam is (Round to three decimal places as needed.) Does this statistic indicate that the proportion of students who passed at least one advanced math or science exam is less than the 44% success rate for microeconomics? Support your assertion. O A. No, because the sample proportion is less than 0.44. O B. Yes, because the sample proportion is less than 0.44. O C. No, because the sample proportion is greater than 0.44 O D. Yes, because the sample proportion is greater than 0.44. b. Calculate a 99% confidence interval for the proportion of those students who passed at least one advanced math or science exam. The 99% confidence interval estimate is (Round to three decimal places as needed. Use ascending order.)

Answer 1

To calculate the proportion of students passing at least one advanced math or science exam, divide the number of students who passed by the total number of students in the sample. The proportion is less than the 44% success rate for microeconomics. The 99% confidence interval estimate is approximately (0.066, 0.142).

Step-by-step explanation:

To calculate the proportion of students who passed at least one advanced math or science exam, we divide the number of students who passed at least one exam by the total number of students in the sample. In this case, 26 students passed at least one exam out of a sample of 250 students. So the proportion is 26/250 = 0.104.

This statistic indicates that the proportion of students who passed at least one advanced math or science exam is less than the 44% success rate for microeconomics. This is because 0.104 is less than 0.44.

Therefore, the correct answer is A. No, because the sample proportion is less than 0.44.

To calculate a 99% confidence interval for the proportion of students who passed at least one advanced math or science exam, we can use the formula:

CI = sample proportion ± (critical value) × √((sample proportion × (1 - sample proportion)) / sample size)

Using the given information, the sample proportion is 0.104, the critical value for a 99% confidence level is approximately 2.576, and the sample size is 250. Plugging these values into the formula:

CI = 0.104 ± (2.576) × √((0.104 × (1 - 0.104)) / 250)

Calculating the values, the 99% confidence interval estimate is approximately (0.066, 0.142).

Answer 2

Exercise a

The proportion of those students who passed at least one math or science exam is 10.4%.

The correct choice is:

B. Yes, because the sample proportion is less than 0.44.

Exercise b

The 99% confidence interval estimate is (0.054, 0.154).

Step-by-step explanation:

There are 250 students.

a. If 26 of the students in the sample passed at least one advanced math or science exam, calculate the proportion of those students who passed at least one math or science exam.

This is
`p = (26)/(250) = 0.104`

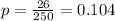
The proportion of those students who passed at least one math or science exam is 10.4%.

Does this statistic indicate that the proportion of students who passed at least one advanced math or science exam is less than the 44% success rate for microeconomics?

Yes, it is. The success rate in this sample is just 10.4%, that is, less than 44%.

The correct choice is:

B. Yes, because the sample proportion is less than 0.44.

b. Calculate a 99% confidence interval for the proportion of those students who passed at least one advanced math or science exam.

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence interval
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

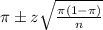
In which

Z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

From a), we found that
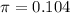`\pi = 0.104`. We also have that
`n = 250`.

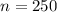We want a 99% confidence interval.

So
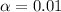`\alpha = 0.01`, z is the value of Z that has a pvalue of
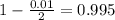`1 - (0.01)/(2) = 0.995`, so z = 2.575.

The lower limit of this interval is:

`\pi - z\sqrt{(\pi(1-\pi))/(250)} = 0.104 - 2.575\sqrt{(0.104*0.896)/(250)} = 0.054`

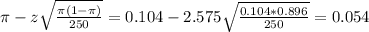
The upper limit of this interval is:

`\pi + z\sqrt{(\pi(1-\pi))/(250)} = 0.104 + 2.575\sqrt{(0.104*0.896)/(250)} = 0.154`

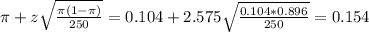
The 99% confidence interval estimate is (0.054, 0.154).