Question

A 0.22LR caliber bullet has a mass of 38 grains (2.50 g) and a muzzle velocity of 1260 ft/s (380 m/s). The bullet is fired into a door made of a double thickness of pine boards, each with a thickness of 0.75 in. The average stopping force exerted by the wood is 960 N. How fast (in m/s) would the bullet be traveling after it penetrated through the door?

Answer 1

`v=339.3217\,m.s^(-1)`

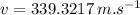
Step-by-step explanation:

mass of the bullet,
`m= 2.5\,g`

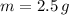
muzzle velocity,
`v=380\,m.s^(-1)`

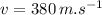
total thickness of the board on which the target is taken,
`s=1.5 * 25.4 \,mm= 38.1* 10^(-3)\,m`

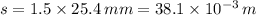
average stopping force by the board,
`F=960 \,N`

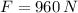
We know,

`F=m.a`

`960=2.5* 10^(-3)* a`

`a= 3.84* 10^5 \,m.s^(-2)`

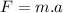
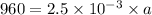
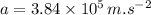
This "a" is the deceleration of bullet in the board material.

Now using the equation of motion,

`v^2=u^2-2a.s`

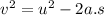
-ve sign, because a is deceleration

`v^2=380^2-2* 3.84* 10^5* 38.1* 10^(-3)`

`v=339.3217\,m.s^(-1)`

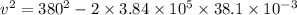
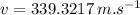
is the velocity when it exits the board material.