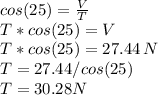Question

A 5.6 kg flower pot is suspended by two chains from the ceiling. The chains make an angle of 25° with

the vertical, Determine the tension in the chains.

Answer 1

Tension on each chain: 30.28N

Step-by-step explanation:

We start by drawing a free-body diagram of all the forces acting on the flower pot. These are:

1) the weight of the flower pot which is the product of the pot's mass time the acceleration of gravity "g" (pictured in green and represented by
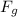`F_g` in the diagram), and

2) the two tensions in the chains, which since they are symmetric, are of the same size, pictured in red color and represented by the letter "T" in the diagram.

We also decompose the tensions T in two components each (a vertical component V and a horizontal component h) which are pictured in blue.

All vertical forces must cancel out since the object is in static equilibrium, so:

`V+V=F_g\\2V=5.6*9.8 N=54.88N\\V=27.44N`

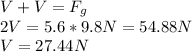
The horizontal components h are equal, and since they act in opposite directions, they indeed cancel out.

Now to calculate the tension, we use the fact that we know the angle between T and the component V. They in fact are related via the cosine of the angle because they are the hypotenuse and the adjacent side in a right angle triangle:

`cos(25)=(V)/(T) \\T*cos(25)=V\\T*cos(25)=27.44\,N\\T=27.44/cos(25)\\T=30.28 N`