Question

Supposeanairportmetaldetectorcatchesaperson with metal 99% of the time. That is, it misses detecting a person with metal 1% of the time. Assume independence of people carrying metal. What is the probability that the first metal-carrying person missed (not detected) is among the first 50 metal-carrying persons scanned?

Answer 1

0.395 or 39.5% probability that the first metal-carrying person missed (not detected) is a

Explanation:

The easiest way to solve this problem is to determine the probability of all 50 of the first 50 metal-carrying people scanned being caught by the metal detector (P(C)). Then, the probability that the first metal-carrying person missed is within the first 50 (P(M)) is 100% minus the probability of all 50 being caught:

`P(C) = 0.99^(50)\\P(C) = 0.605`

`P(M) = 1- P(C) \\P(M)= 1- 0.605\\P(M)=0.395`

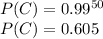
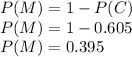
There is a 0.395 or 39.5% probability that the first metal-carrying person missed (not detected) is among the first 50 metal-carrying people scanned.