Question

Consider three charged sheets, A, B, and C. The sheets are parallel with A above B above C. On each sheet there is surface charge of uniform density: −4 · 10−5 C/m2 on A, 7 · 10−5 C/m2 on B, and −3 · 10−5 C/m2 on C. (The density given includes charge on both sides of the sheet.) What is the magnitude of the electrical force per unit area on each sheet? Check to see that the total force per unit area on the three sheets is zero.

Answer 1

0.

Step-by-step explanation:

To find the electrical force per unit area on each sheet we start defining our variables,

`\sigma_A = -4.10^(-5)C/m^2`

`\sigma_B= -7.10^(-5)C/m^2`

`\sigma_C = -3.1^(-5)C/m^2`

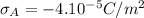
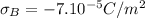
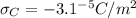
We find the electric field for each one, this formula is given by,

`E= (\sigma_i)/(2\epsilon_0)`

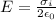
Substituting each value from the three charged sheets, we have

`E_A= (-4.10^(-5)C/m^2)/(2\epsilon_0)(\hat{j})`

`E_B= (-7.10^(-5)C/m^2)/(2\epsilon_0)(-\hat{j})`

`E_C= (-3.1^(-5)C/m^2)/(2\epsilon_0)(\hat{j})`

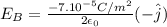
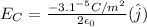
The electric field is

`E_(NET)= E_A+E_B+E_C`

`E_(NET)=(-4.10^(-5)C/m^2)/(2\epsilon_0)(\hat{j})+(-7.10^(-5)C/m^2)/(2\epsilon_0)(-\hat{j})+ (-3.1^(-5)C/m^2)/(2\epsilon_0)(\hat{j})`

`E_(NET) = 0`

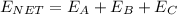
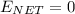
Force on each sheet is,

`F=E_(NET)\sigma ds`

`F=0`

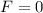
The total force is 0