Answer:
The required elasticity is
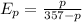 .
.
The demand is inelastic.
The required value of p for which total revenue is maximum is 178.5
Explanation:
Consider the provided function.
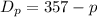
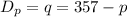
Part (A) The elasticity
The elasticity of demand is:


But elasticity is always positive therefore,
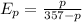
Hence, the required elasticity is
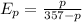 .
.
Part (b) The elasticity at p=89, stating whether the demand is elastic, inelastic or has unit elasticity.
Substitute p=89 in above elasticity formula.
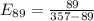

The above value is less than 1, therefore the demand is inelastic.
Part (C) The value(s) of p for which total revenue is a maximum (assume that p is in dollars).
For maximum revenue substitute E=1.
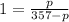
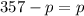

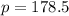
Hence, the required value of p for which total revenue is maximum is 178.5